📌 この記事でわかること:
- DTWとTimeSeriesKMeansの使いどころと考え方
- Pythonコードでの実装例(株価分析ベース)
- 時系列クラスタリングの実務での注意点とコツ
👤 対象となる読者:
- Pythonを学び中の初〜中級者
- 株価データなどを使って“動きの似たパターン”を分類したい人
🔧 活用できるシーン:
- ポートフォリオ分析
- 異常検知(製造、IoT)
- ユーザー行動の分類
1. はじめに
「科学的に、似た動きをするデータを分類したい」。 そう考えてコードを書いていると、ある時点で DTW や TimeSeriesKMeans に行き着く人は多いはずです。
私自身の例で言えば、 株価データを取得し、ポートフォリオの構成を計算する中で 「似た動きをする銘柄を分類したい」という需要が生まれました。
この記事は、そんな分析ニーズに対して、DTWとTimeSeriesKMeansが どう役立つのかを整理して解説することを目的としています。
DTWとTimeSeriesKMeansは、似た動きをする時系列データを 「ずれ」をも考慮しつつ、分類する技術です。
2. DTWとTimeSeriesKMeansの概要
短くいうと…
- DTW: 時間的にずれても動きが似ていれば「似てる」と判断してくれる技術
- TimeSeriesKMeans: DTWで決めた近さを利用して、似た動きをするデータを同じグループに分ける方法
これを使うと、価格の大小やタイミングの違いに左右されにくい「動きの似たデータ」を見つけることができます。
3. 株価データ分析での活用
この記事では、私自身が株価データを使って分析したケースをもとに、実装と解説を行っています。
実際の例はこちら:
👉 Pythonで資産リバランス:リスクに基づく最適な構成比とは?
4. 仕組みを説明する
実際に株価データへクラスタリングを適用する前に、まずは “TimeSeriesKMeans + DTW” がどういう基準で似た動きを分類しているのか、感覚的に理解しておきましょう。
今回は、あえて極端な動きを持つ5つの時系列データを用意し、分類結果を図で見てみます。
4.1 分類前:元の5時系列データ
以下の図は、正規化された5種類の時系列データを示しています。 それぞれの波形は異なる特徴(周期性、直線、ステップ変化など)を持っています。
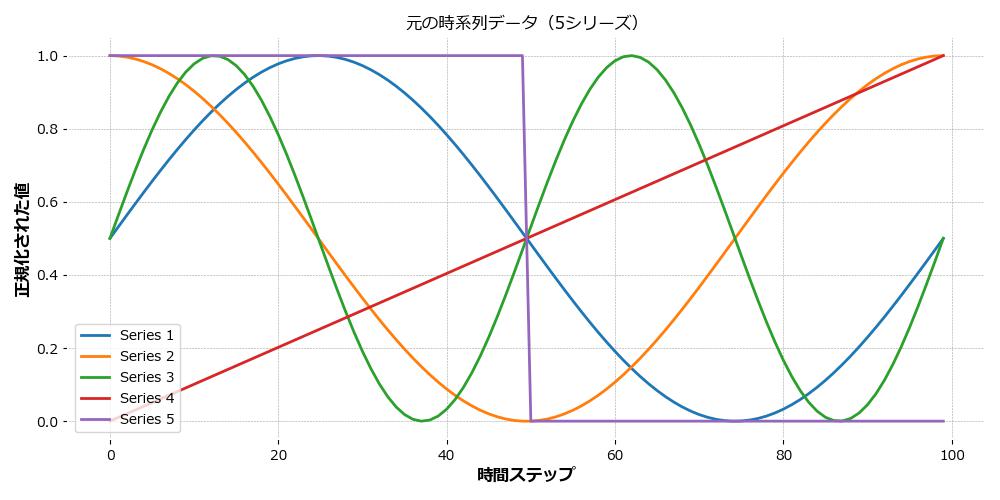
- Series 1:sin波(周期性)
- Series 2:cos波(周期性)
- Series 3:2倍周期のsin波
- Series 4:直線的な増加
- Series 5:ステップ関数(途中で急変)
これらは見た目でも動きの違いがはっきりしています。
4.2 分類結果:3クラスタに分けてみる
これら5つの時系列データを、DTW(Dynamic Time Warping)を距離指標とし、TimeSeriesKMeansで3つのクラスタに分類しました。
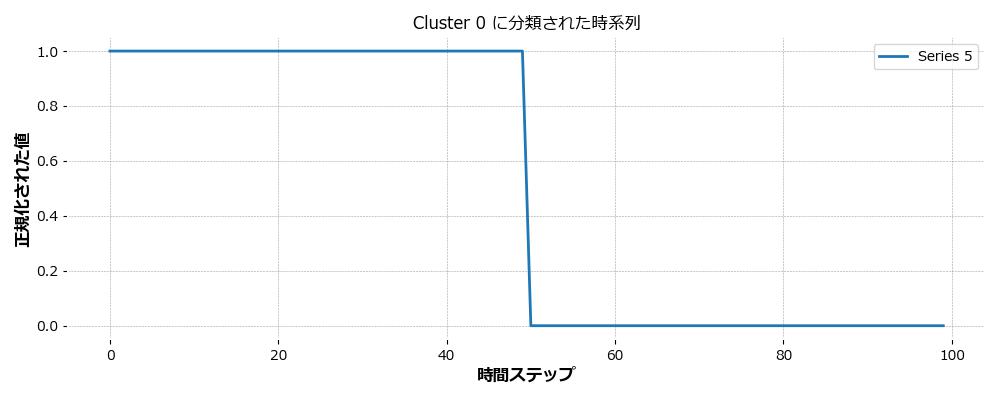
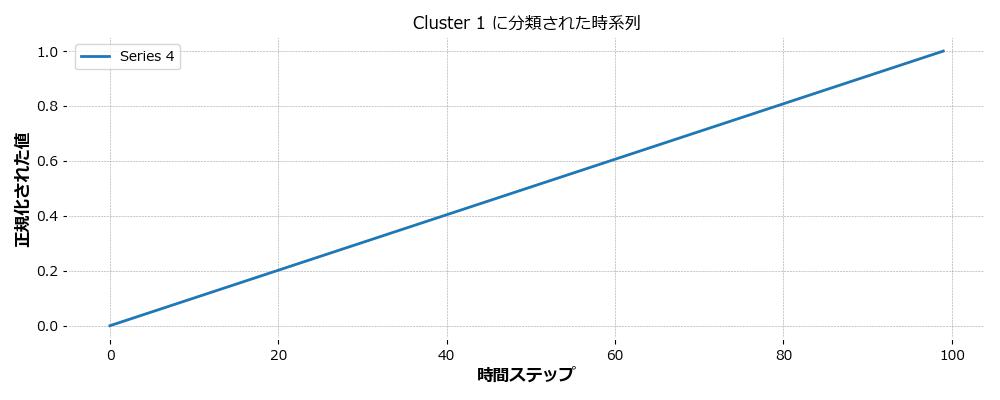
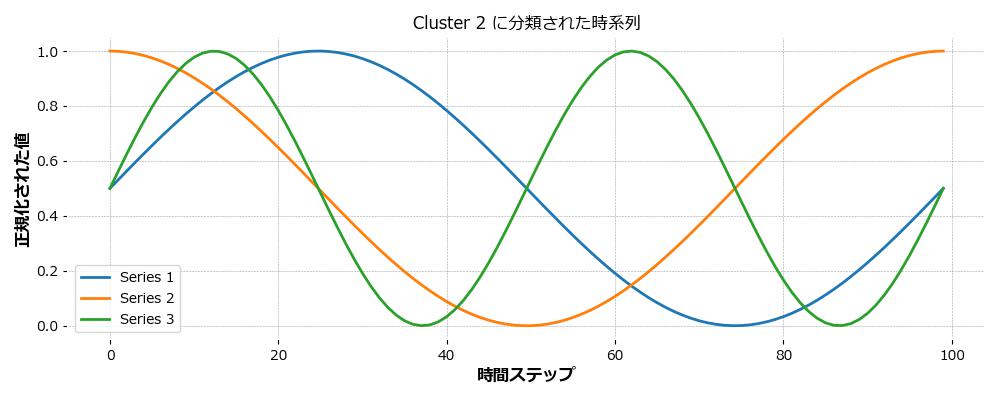
- Cluster 0:周期性を持つ3つの波形(sin、cos、倍速sin)
- Cluster 1:直線的に増加するSeries 4
- Cluster 2:急激なステップ変化を持つSeries 5
4.3 DTWによるマッチングのイメージ
DTW(Dynamic Time Warping)の特徴は、時間軸の“ずれ”を吸収して、時系列の類似性を測る点にあります。
ここでは、以下のような2つのデータを例に解説します:
- Series A:山が2箇所(中央寄りにピーク)
- Series B:同じ山の形を持つが、時間軸が少し後ろにずれ、スケールも上下に違いがある
このように、形状は似ているが、位相(タイミング)・高さ・スケールが異なる2つの波形があるとします。
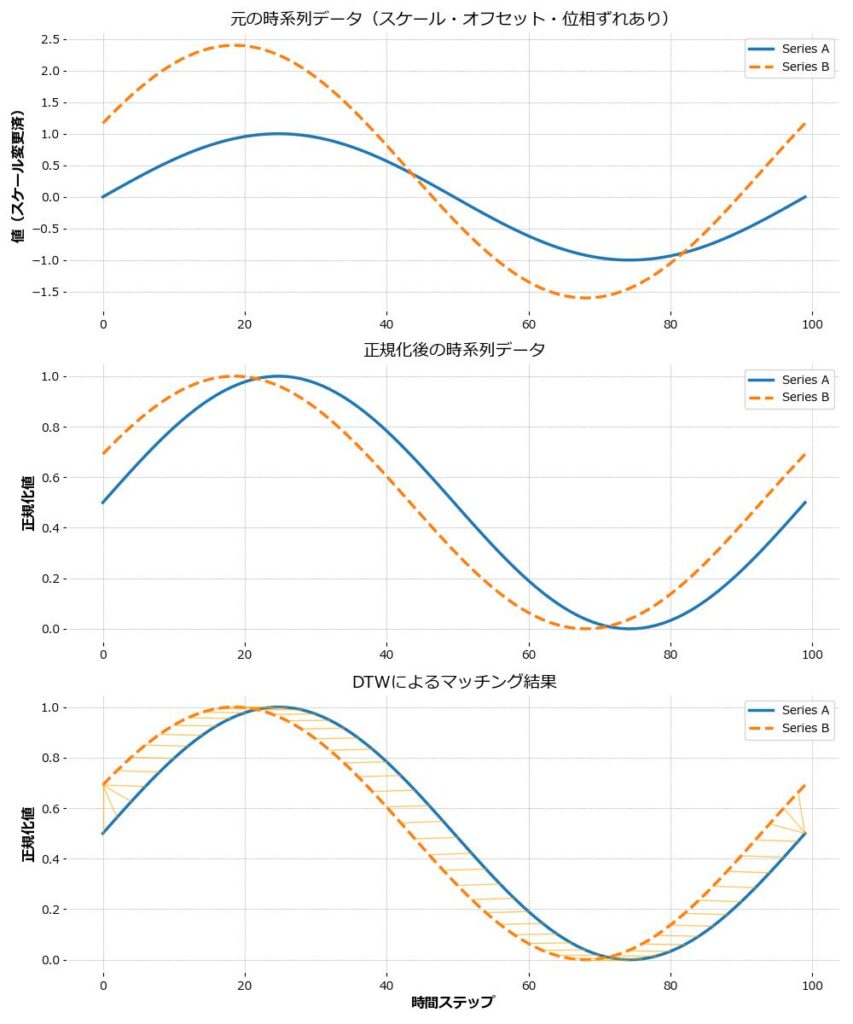
図①:元のSeries AとSeries B
この図では、Series A/B の「ずれ」が視覚的に確認できます。
図②:正規化されたSeries AとB
MinMaxScaler などでスケーリングを行い、異なる値幅を0〜1に揃えた状態です。 これにより「形」の違いに注目しやすくなります。
図③:DTWでマッチングされたAとB
DTWは「対応点」を動的にずらしながら、最も類似するパスを見つけ出します。 図中のグレーの線が「Series Aのどの点と、Series Bのどの点が対応付けられたか」を示しています。
このように、DTWは「同じ時間位置の比較」に限定せず、 時間を“伸び縮み”させながら、構造的に似ている動き同士を見つけ出します。
4.4 この図の位置づけ
今回の図はあくまで仕組みの可視化と直感の理解を目的としており、実際の株価ではここまで明確に分類できるケースは多くありません。
とはいえ、「どのような基準で似ていると判断するか」を知ることで、TimeSeriesKMeans + DTWの動作に納得感を持って使うことができます。
次章では、実際の株価データにこの考え方を適用し、どのようにクラスタリングできるかを見ていきましょう。
5. TimeSeriesKMeansのパラメータと注意点
5.1 TimeSeriesKMeansの書き方(構文・引数解説)
TimeSeriesKMeans(
n_clusters=4, # クラスタ数:分類するグループの数。いくつに分けるか?
metric="dtw", # 距離指標:"euclidean"(ユークリッド距離)も選べる。どんな基準で「近い」と判断するか?
max_iter=10, # 最大反復回数:グループ分けの計算を何回まで繰り返すか?
random_state=0 # 再現性のためのシード値:同じ結果を出したいときの乱数制御。
)5.2 パラメータ入力の注意点
パラメータの意味を知らずに値を入れると、実行時にエラーが発生することがあります。以下に代表的な例を挙げます:
| パラメータ | 型 / 許容値 | 誤設定例 | エラーの可能性 |
|---|---|---|---|
n_clusters | 正の整数 | 0, -1, None | ValueError: Number of clusters must be > 0 |
metric | “dtw” or “euclidean” | “manhattan” | ValueError: Unknown metric name |
max_iter | 正の整数 | “10”(文字列) | TypeError: Expected int |
random_state | int or None | float(‘inf’) | TypeError: Cannot convert float to int |
正しい入力の知識がないと、コードは“クラッシュ”します。 特に random_state=∞ のような指定は完全に無効で、実行時エラーになります。
コードは正しい型や値を指定しないとエラーになるため、表を参考に安全な設定を心がけましょう。
6. 実装の流れ(コードでやっていることの意味)
① yfinance で株価取得:銘柄ごとの価格データを過去にさかのぼって取得します。
② MinMaxScaler で正規化:銘柄ごとの価格の大小を0〜1のスケールに揃えます。
③ TimeSeriesKMeans(metric="dtw") で分類:「動きが似ているもの同士」をグループに分けます。
④ グラフ表示:分類結果を視覚化し、クラスタごとにどんな傾向があるかを見ます。この流れで、単に「似てそう」ではなく、「統計的に動きが似ている」と言える銘柄を分類・視覚化できるようになります。
7. その他の手法との比較
DTW x TimeSeriesKMeans以外にも、次のような手法があります:
- 「距離の機構」:ユークリッド距離 / コサイン類似度 / Soft-DTW / Frechet距離
- 「分類手法」: DBSCAN / 階層クラスタリング / GMM / HMM
興味がある方は、ぜひ各手法を調べて比較してみてください!
8. おわりに
DTWもTimeSeriesKMeansも、時系列データ分析の強力な武器です。
もっと理解したい人も、さらっと再確認したい人も、実用の前に一度立ち止まって仕組みを整理してみると、 分析の精度が一段と上がるはずです。










コメント