Pythonで資産リバランス：リスクに基づく最適な構成比とは？

2025年3月31日2025年4月5日

📌 この記事でわかること：

Pythonでポートフォリオを「リスクベース」で調整する方法
リスクに基づいた構成比の算出と調整（コード付き）
買い・売り・両方の3モードでリバランスの違いを可視化

👤 対象となる読者：

ETFや個別株の配分が適正か不安な人
「感覚」ではなく「数値」でバランスを見たい人
Pythonで資産分析をしてみたい中級者〜独学勢

🔧 活用できるシーン：

新しい銘柄を組み入れるときの構成バランス検討
「今の構成って偏ってない？」とチェックしたいとき
投資信託・ETFのリバランス戦略を考えるとき

🔄 次は実践へ：どうリバランスする？

ここまでで、

自分のポートフォリオにどんな性質の銘柄があるか
どんなクラスタに偏っているか
どのカテゴリが多すぎて、どれが足りないか

といった“現在地”が可視化されました。

👉 まだ前編を読んでいない方はこちらから：
【前編】クラスタ分析とリスク評価から始めるポートフォリオ分析

でも、「気づき」だけで終わってはもったいないですよね。
次は、「じゃあ実際にどう調整するか？」という具体的な行動に落とし込んでいきます。

1. Pythonコードとその条件・補足説明

この記事では、3つの主要なコードスニペットを使用しています。それぞれのコードには明確な目的と前提条件があります。

✅ コード①：クラスタリングとリスク分析（ベース分析）

目的：銘柄間の値動きパターンを比較し、クラスタ分類とリスク計測を行う
前提：
- 使用銘柄：SPYD, HDV, QQQ, VOO, VTI, MSFT, NVDA, RGTI
- 分析期間：2022/01/01 ～ 2024/12/31（変更可能）
- 株価は「終値（Close）」を使用
出力：
- 相関マトリクス（ヒートマップ）
- クラスタ別の銘柄分類（4クラスタ）
- 各クラスタの値動き（正規化済）
- 各クラスタの平均パターン
- リスク（標準偏差）ランキング

📌 補足：クラスタ数（n_clusters）は自由に変更可能で、視覚的に類似銘柄を把握するために有効です。
※なお、期間設定はRGTIの上場時期（2022年）以降に合わせています。

　RGTIなど新興銘柄を含めない場合は、より長期の分析も可能です。

✅ コード②：エルボー法による最適クラスタ数の決定

目的：最適なクラスタ数を自動的に見つける
前提：
- 使用銘柄・期間はコード①と同様
- 0〜1にスケーリングされた株価を使用
- 最大クラスタ数（max_k）は任意設定（例：6）
出力：
- クラスタ数とSSE（誤差平方和）の関係を示すエルボーグラフ

📌 補足：クラスタ数を適当に決めたくない場合、こちらのエルボー法を先に実行し、最も自然な“ひじ”の位置（変化の急減点）を選びましょう。

✅ コード③：リスクベースのポートフォリオ構成比（可視化付き）

目的：各銘柄のリスクに応じた構成比を算出し、現在との乖離を比較・可視化する
前提：
- 現在の保有金額（任意入力）
- 各銘柄のリスク（標準偏差）
- 各銘柄のクラスタ・カテゴリ（任意設定）
出力：
- 現在 vs 目標（棒グラフ）
- 現在 vs 目標の円グラフ（構成比）
- クラスタ別構成比（現在・目標）
- カテゴリ別構成比（現在・目標）

📌 補足：リスクは過去データから計算した値を用いています。将来の変化があるため、定期的な見直しが前提です。

🔁 各コードのつながり

コード①でリスク・クラスタを分析
コード②でクラスタ数の最適化をサポート（任意）
コード③で自分のポートフォリオに応じたリスクベース調整を実施

このように、分析→最適化→活用という流れでつながっています。

🛠️ カスタマイズ可能なポイント

対象銘柄の変更（自由）
分析期間の変更（柔軟）
リスクや構成金額の入力（あなたのポートフォリオに応じて）
クラスタ/カテゴリの設定（好みに応じて分類可能）

次の章では、これらのコードをそのままコピペで使えるようにフル公開します。分析結果と合わせて、ぜひ自分の環境で試してみてください！

2. 銘柄のクラスタ分析とリスク評価

この章では、ポートフォリオ構成の第一歩として、保有・検討中の銘柄についてクラスタ分析とリスク評価を行います。目的は、各銘柄がどのような値動きをしているのか、どの銘柄と似た傾向を持っているかを把握し、分散投資の参考にすることです。

🔧 使用条件（今回の設定）

対象銘柄：SPYD, HDV, QQQ, VOO, VTI, MSFT, NVDA, RGTI
分析期間：2022年1月1日〜2024年12月31日
分類手法：時系列クラスタリング（TimeSeriesKMeans + DTW）
クラスタ数：4（今回は手動で指定）

※分析期間が短めなのは、RGTIの上場時期に合わせているためです。

💻 フルコード①：クラスタリングとリスク分析

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from tslearn.clustering import TimeSeriesKMeans
from tslearn.utils import to_time_series_dataset
from sklearn.preprocessing import MinMaxScaler

# --------- 🔧 設定エリア ---------
tickers = ["SPYD", "HDV", "QQQ", "VOO", "VTI", "MSFT", "NVDA", "RGTI"]
start_date = "2022-01-01"
end_date = "2024-12-31"
n_clusters = 4  # ← クラスタ数変更可能！

# --------- 📈 データ取得 ---------
data = yf.download(tickers, start=start_date, end=end_date)["Close"]
data = data.dropna()
scaler = MinMaxScaler()
scaled_data = pd.DataFrame(scaler.fit_transform(data), index=data.index, columns=data.columns)

# --------- 📊 相関ヒートマップ ---------
plt.figure(figsize=(10, 8))
sns.heatmap(data.pct_change().corr(), annot=True, cmap="coolwarm", vmin=-1, vmax=1)
plt.title("□ 株式間の相関係数マトリクス", fontsize=14)
plt.show()

# --------- 🤖 クラスタリング ---------
ts_dataset = to_time_series_dataset([scaled_data[col].values for col in scaled_data.columns])
model = TimeSeriesKMeans(n_clusters=n_clusters, metric="dtw", max_iter=10, random_state=0)
clusters = model.fit_predict(ts_dataset)

# --------- 🧠 クラスタ分類表示 ---------
cluster_map = {}
for i in range(n_clusters):
    cluster_map[i] = [ticker for j, ticker in enumerate(scaled_data.columns) if clusters[j] == i]
print("\n🧠 クラスタごとの分類:")
for cid, tickers_in in cluster_map.items():
    print(f"Cluster {cid}: {tickers_in}")

# --------- 📉 各クラスタの動き ---------
for i in range(n_clusters):
    cluster_tickers = cluster_map[i]
    plt.figure(figsize=(10, 6))
    for ticker in cluster_tickers:
        plt.plot(scaled_data.index, scaled_data[ticker], label=ticker)
    plt.title(f"□ Cluster {i} に属する銘柄の動き（正規化）", fontsize=14)
    plt.legend()
    plt.show()

# --------- 🧮 クラスタ中心の平均パターン ---------
plt.figure(figsize=(10, 6))
for i in range(n_clusters):
    plt.plot(model.cluster_centers_[i].ravel(), label=f"Cluster {i}")
plt.title("□ クラスタの代表的な動き（平均パターン）", fontsize=14)
plt.xlabel("時間ステップ")
plt.ylabel("正規化株価")
plt.legend()
plt.show()

# --------- ⚠️ リスク分析（標準偏差） ---------
returns = data.pct_change().dropna()
risk = returns.std().sort_values(ascending=False)
print("\n📊 リスク（標準偏差）ランキング:")
print(risk)

🧠 クラスタごとの分類

Cluster 0: ['RGTI']
Cluster 1: ['NVDA']
Cluster 2: ['MSFT', 'QQQ', 'SPYD', 'VOO', 'VTI']
Cluster 3: ['HDV']

それぞれのクラスタには、値動きの類似性が高い銘柄がまとめられています。たとえば、RGTIやNVDAといった高ボラティリティ銘柄が単独クラスタに分類されており、明確に他と異なる動きをしていることがわかります。

補足分析：ヒートマップからの読み取り

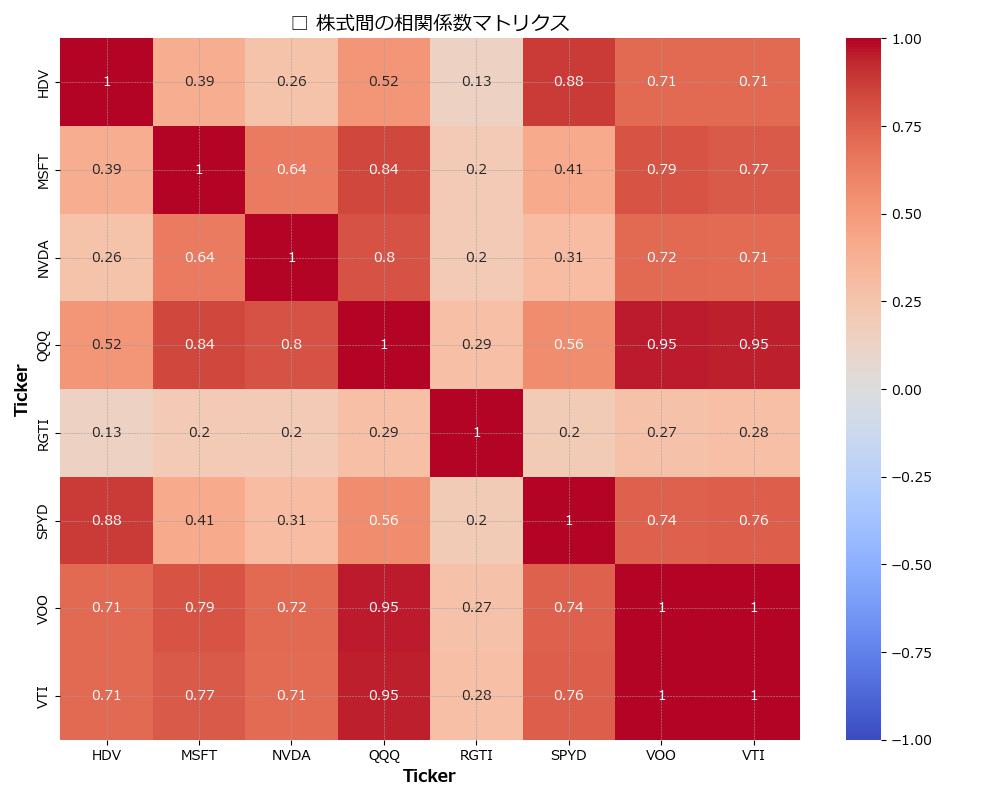
VOO・VTI・QQQ の相関が非常に高く（0.95）、インデックス構成銘柄が被っているため、動きも一致。
MSFT・QQQ も強い相関（0.84）。QQQ はナスダック100であり、MSFTは主要構成銘柄。
SPYD・HDV は高配当ETF同士で相関が高い（0.88）。
RGTI はどの銘柄とも相関が非常に低く、他と異なる動き。

補足分析：クラスタ平均パターンからの読み取り

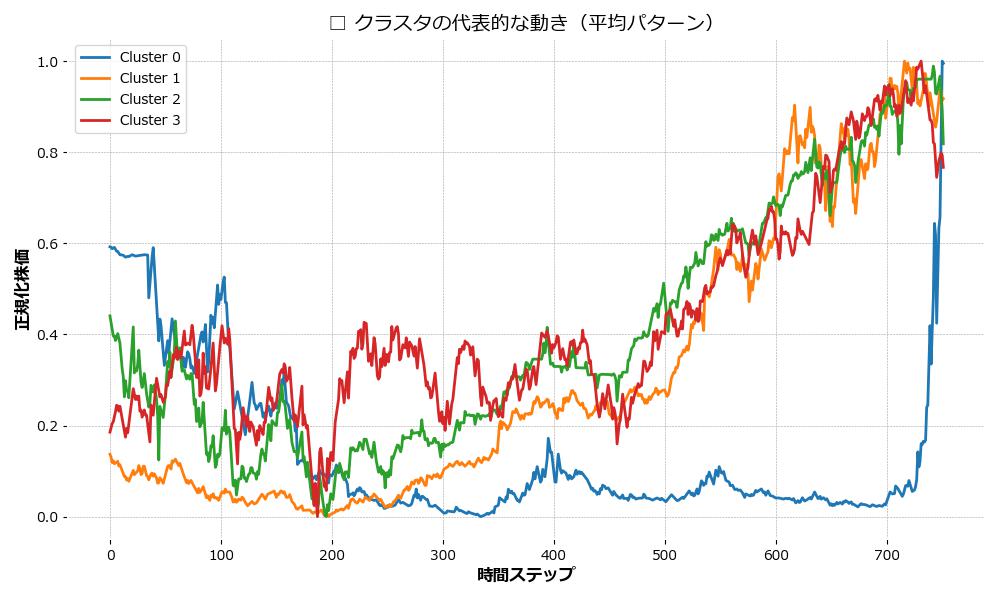
Cluster 0（RGTI）：上下動が大きく、非常に高いボラティリティ
Cluster 1（NVDA）：中盤まで低調、後半で大きく上昇するグロース株らしい動き
Cluster 2（MSFT, QQQ, SPYD, VOO, VTI）：比較的安定した成長を示す王道資産群
Cluster 3（HDV）：価格の変動が少なく、ディフェンシブな傾向

🔍 補足：コードでは、各Clusterごとの銘柄の動きも出力します！気になる方は試してみてね！

📊 リスク（標準偏差）ランキング

RGTI    0.086179
NVDA    0.034828
MSFT    0.017381
QQQ     0.014948
VTI     0.011345
VOO     0.011010
SPYD    0.010649
HDV     0.008406

この結果から、RGTIやNVDAのようなグロース銘柄のリスクが高く、HDVなどのディフェンシブ銘柄は安定している傾向にあることが確認できます。

🔄 次章へのつなぎ

今回はクラスタ数を4と設定しましたが、これは果たして最適だったのでしょうか？次章では「エルボー法」を用いて、クラスタ数の最適化を検証していきます。

3. 最適なクラスタ数の検証（エルボー法）

現在前章では、クラスタ数を “4” に手動で設定してクラスタリングを実施しました。結果として、RGTI や NVDA のような異質な動きをする銘柄が単独クラスタに分類されるなど、一定の納得感がある分類が得られました。

しかし、「クラスタ数4」は本当に最適だったのでしょうか？

この章では、エルボー法（Elbow Method） を使って、データに基づく最適なクラスタ数を検証していきます。

📌 エルボー法とは？

クラスタ数を変化させながらクラスタリングを繰り返し、クラスタ内の誤差（SSE）を記録していきます。クラスタ数が多くなるほど誤差は小さくなりますが、ある時点から改善幅が小さくなります。

この「改善の頭打ちになる点」がひじ（エルボー）のように見えるため、最適なクラスタ数の目安として利用されます。

💻 フルコード②：クラスタ数の最適化（エルボー法）

# 必要なライブラリ
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from tslearn.clustering import TimeSeriesKMeans
from tslearn.utils import to_time_series_dataset
from sklearn.preprocessing import MinMaxScaler
from tqdm import tqdm

# 1. 設定（ティッカーと期間）
tickers = ["SPYD", "HDV", "QQQ", "VOO", "VTI", "MSFT", "NVDA", "RGTI"]
start_date = "2022-01-01"
end_date = "2025-01-01"

# 2. データ取得と整形
data = yf.download(tickers, start=start_date, end=end_date)["Close"]
data = data.fillna(method="ffill").dropna()

# 3. 正規化（0～1スケーリング）
scaler = MinMaxScaler()
scaled_data = pd.DataFrame(scaler.fit_transform(data), columns=data.columns, index=data.index)

# 4. エルボー法でクラスタ数の最適化
def find_optimal_clusters(data, max_k=8):
    ts_dataset = to_time_series_dataset([data[col].values for col in data.columns])
    distortions = []
    for k in tqdm(range(1, max_k + 1), desc="クラスタ数を評価中"):
        model = TimeSeriesKMeans(n_clusters=k, metric="dtw", max_iter=10, random_state=0)
        model.fit(ts_dataset)
        distortions.append(model.inertia_)
    return distortions

distortions = find_optimal_clusters(scaled_data, max_k=6)

# 5. エルボーグラフ表示
plt.figure(figsize=(8, 5))
plt.plot(range(1, 7), distortions, marker='o')
plt.title("□ クラスタ数の最適化（エルボー法）", fontsize=14)
plt.xlabel("クラスタ数")
plt.ylabel("SSE（誤差平方和）")
plt.xticks(range(1, 7))
plt.grid(True)
plt.tight_layout()
plt.show()

📉 クラスタ数ごとの誤差（SSE）の推移

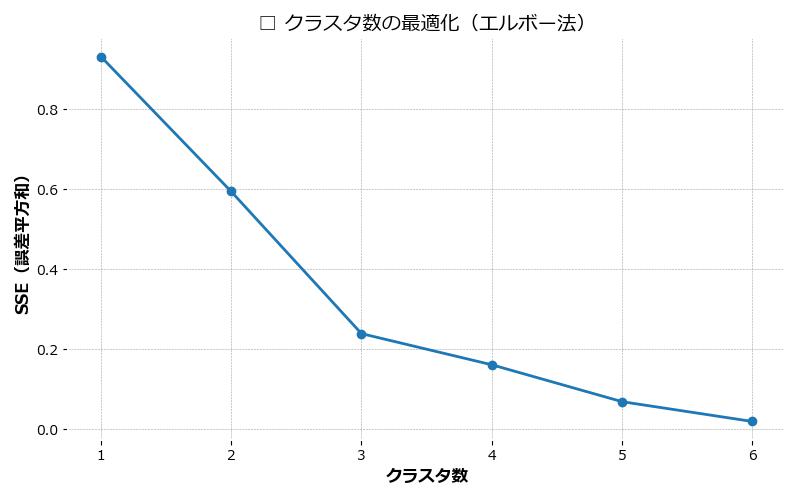
上のグラフでは、クラスタ数を 1 〜 6 に変化させたときの誤差（SSE）の推移を示しています。たとえば、以下のような傾向が読み取れます：

クラスタ数が 1 → 2 → 3 に増えると、誤差は大きく改善する
4〜5あたりからは誤差の改善幅が緩やかになる

このことから、クラスタ数として 3〜4あたりが妥当な候補 と判断できます。

🔍 補足：クラスタ数の選び方は目的次第

「分類の精度」よりも、「使いやすさ」「意味のあるまとまり」を重視する場合、**少なめのクラスタ数（3〜4）**が望ましいこともあります。
今回のように「ポートフォリオの傾向を把握する」目的であれば、クラスタ数4程度でも十分と考えられます。

⏭ 次章へのつなぎ

次章では、このクラスタ分析やリスクを踏まえた上で、実際のポートフォリオ調整に入っていきます。

4. 調整モード別ポートフォリオ変化の比較（Before / Adjust / After）

🎯 本章の目的

ポートフォリオをリスクベースでリバランスする際に、

買い増しのみ（buy）
売却のみ（sell）
買い・売り両方（both） という3つのモードでの違いを比較します。

「売却は避けたい」「資金を追加できる」「なるべく手を加えたくない」など、状況は人それぞれ。それぞれの戦略で、どのようにポートフォリオが変化するのかを見ていきましょう。

🔧 分析条件

対象銘柄：HDV, VOO, TLT, VTI, QQQ, MSFT, RGTI
各銘柄のリスク：標準偏差ベース（過去の価格変動をもとに計算）
保有金額：筆者の仮想保有額をもとに設定
クラスタ/カテゴリ：前章の分析結果より仮設定
リバランス方法：逆リスク重み（リスクが低いほど比重を大きく）

💻 フルコード③：

import pandas as pd
import matplotlib.pyplot as plt

# ✅ モード選択: "buy", "sell", "both"
mode = "both"
print(f"\n選択モード: {mode}\n")

# ✅ 現在の保有資産
current_portfolio = {
    "HDV": 1000,
    "VOO": 3000,
    "TLT": 0,
    "VTI": 0,
    "QQQ": 5000,
    "MSFT": 2000,
    "RGTI": 500
}

# ✅ 銘柄ごとのリスク（標準偏差）
risk = {
    "HDV": 0.008402,
    "VOO": 0.011004,
    "TLT": 0.011210,
    "VTI": 0.011338,
    "QQQ": 0.014941,
    "MSFT": 0.017372,
    "RGTI": 0.086209
}

# ✅ 銘柄ごとのクラスタ（仮設定）
clusters = {
    "HDV": "Cluster 0",
    "VOO": "Cluster 0",
    "TLT": "Cluster 0",
    "VTI": "Cluster 1",
    "QQQ": "Cluster 1",
    "MSFT": "Cluster 2",
    "RGTI": "Cluster 2"
}

# ✅ 銘柄ごとのカテゴリ（仮設定）
categories = {
    "HDV": "高配当",
    "VOO": "インデックス",
    "TLT": "債券",
    "VTI": "インデックス",
    "QQQ": "グロース",
    "MSFT": "グロース",
    "RGTI": "小型成長"
}

# ✅ リスクの逆数で割合計算
total_inv_risk = sum(1 / r for r in risk.values())
weights = {k: (1 / risk[k]) / total_inv_risk for k in risk}

# ✅ ポートフォリオ総額
total_value = sum(current_portfolio.values())

# ✅ 目標金額
target_values = {k: weights[k] * total_value for k in risk}

# ✅ 差額（目標 - 現在）
diff = {k: target_values[k] - current_portfolio.get(k, 0) for k in risk}

# ✅ モード処理（フィルタリング）
if mode == "buy":
    filtered_diff = {k: v if v > 0 else 0 for k, v in diff.items()}
elif mode == "sell":
    filtered_diff = {k: v if v < 0 else 0 for k, v in diff.items()}
else:
    filtered_diff = diff.copy()

# ✅ 調整後金額（After）
after = {k: current_portfolio.get(k, 0) + filtered_diff.get(k, 0) for k in risk}

# ✅ 表の作成
df_adjust = pd.DataFrame({
    "Before ($)": pd.Series(current_portfolio),
    "Adjust ($)": pd.Series(filtered_diff),
    "After ($)": pd.Series(after),
    "Risk (σ)": pd.Series(risk),
    "Cluster": pd.Series(clusters),
    "Category": pd.Series(categories)
}).fillna(0).round(2)

print("📋 調整結果（Before / Adjust / After）")
print(df_adjust)

# ✅ 現在 vs 目標（棒グラフ）
plt.figure(figsize=(10, 5))
plt.bar(df_adjust.index, df_adjust["Before ($)"], label="Before", color='steelblue')
plt.bar(df_adjust.index, df_adjust["After ($)"], label="After", color='darkorange', alpha=0.7)
plt.title("📊 調整前後のポートフォリオ")
plt.ylabel("金額 ($)")
plt.legend()
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()

# ✅ 円グラフ（現在 vs 調整後）
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
df_adjust["Before ($)"].plot.pie(autopct="%1.1f%%", ax=axes[0], title="現在の構成比")
df_adjust["After ($)"].plot.pie(autopct="%1.1f%%", ax=axes[1], title="調整後の構成比")
plt.tight_layout()
plt.show()

# ✅ クラスタ別構成
cluster_before = df_adjust.groupby("Cluster")["Before ($)"].sum()
cluster_after = df_adjust.groupby("Cluster")["After ($)"].sum()

fig, axes = plt.subplots(1, 2, figsize=(12, 6))
cluster_before.plot.pie(autopct='%1.1f%%', ax=axes[0], title='クラスタ別（現在構成）')
cluster_after.plot.pie(autopct='%1.1f%%', ax=axes[1], title='クラスタ別（調整後構成）')
plt.tight_layout()
plt.show()

# ✅ カテゴリ別構成
category_before = df_adjust.groupby("Category")["Before ($)"].sum()
category_after = df_adjust.groupby("Category")["After ($)"].sum()

fig, axes = plt.subplots(1, 2, figsize=(12, 6))
category_before.plot.pie(autopct='%1.1f%%', ax=axes[0], title='カテゴリ別（現在構成）')
category_after.plot.pie(autopct='%1.1f%%', ax=axes[1], title='カテゴリ別（調整後構成）')
plt.tight_layout()
plt.show()

✅ 選択モード: both（買い・売り両方で調整）

Ticker	Before ($)	Adjust ($)	After ($)	Risk (σ)	Cluster	Category
HDV	1000	1615.09	2615.09	0.01	Cluster 0	高配当
VOO	3000	-1003.27	1996.73	0.01	Cluster 0	インデックス
TLT	0	1960.03	1960.03	0.01	Cluster 0	債券
VTI	0	1937.91	1937.91	0.01	Cluster 1	インデックス
QQQ	5000	-3529.42	1470.58	0.01	Cluster 1	グロース
MSFT	2000	-735.21	1264.79	0.02	Cluster 2	グロース
RGTI	500	-245.13	254.87	0.09	Cluster 2	小型成長

🎨 調整の可視化

以下のグラフにより、調整前後の資産構成の変化が一目でわかります。

💹 棒グラフ：調整前後の金額比較

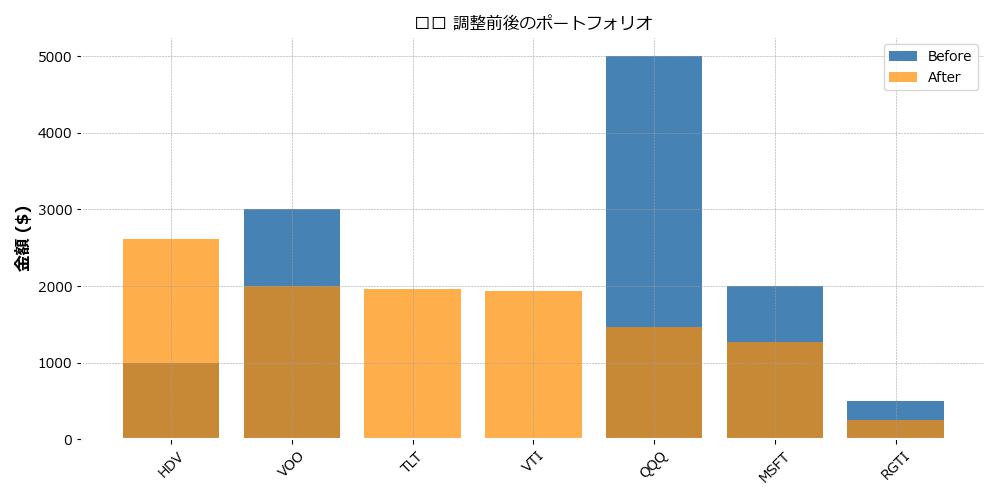
🧩 円グラフ：ティッカー別の構成比（Before / After）

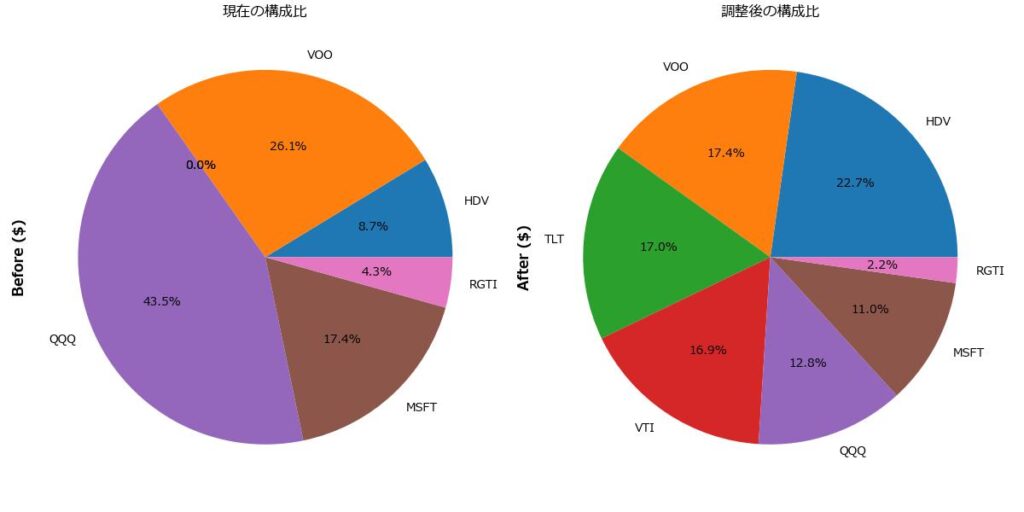
🧠 クラスタ別の構成比（Before / After）

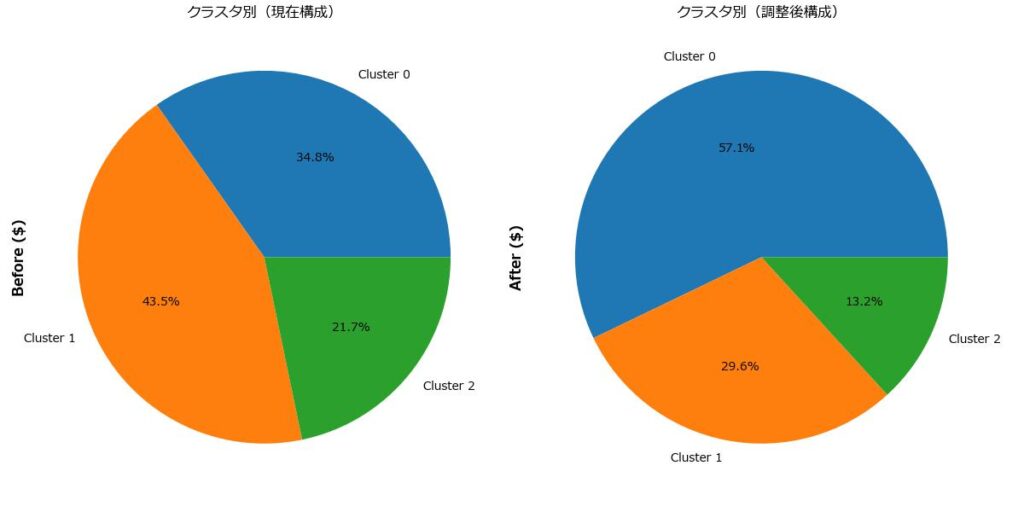
🏷️ カテゴリ別の構成比（Before / After）

以下は「buy」、「sell」のモードです。
グラフの画像は張りませんが、ぜひ気になる方は試してみてね！

✅ 選択モード: buy（売却せず、買い増しでのみ調整）

Ticker	Before ($)	Adjust ($)	After ($)	Risk (σ)	Cluster	Category
HDV	1000	1615.09	2615.09	0.01	Cluster 0	高配当
VOO	3000	0.00	3000.00	0.01	Cluster 0	インデックス
TLT	0	1960.03	1960.03	0.01	Cluster 0	債券
VTI	0	1937.91	1937.91	0.01	Cluster 1	インデックス
QQQ	5000	0.00	5000.00	0.01	Cluster 1	グロース
MSFT	2000	0.00	2000.00	0.02	Cluster 2	グロース
RGTI	500	0.00	500.00	0.09	Cluster 2	小型成長

✅ 選択モード: sell（買い増しせず、売却のみで調整）

Ticker	Before ($)	Adjust ($)	After ($)	Risk (σ)	Cluster	Category
HDV	1000	0.00	1000.00	0.01	Cluster 0	高配当
VOO	3000	-1003.27	1996.73	0.01	Cluster 0	インデックス
TLT	0	0.00	0.00	0.01	Cluster 0	債券
VTI	0	0.00	0.00	0.01	Cluster 1	インデックス
QQQ	5000	-3529.42	1470.58	0.01	Cluster 1	グロース
MSFT	2000	-735.21	1264.79	0.02	Cluster 2	グロース
RGTI	500	-245.13	254.87	0.09	Cluster 2	小型成長

🔍 分析ポイント

Bothモード：最も効率的だが、実行には税制・手数料も考慮する必要あり。
Buyモード：資金追加が可能な人向け。売却益にかかる税金の影響なし。
Sellモード：資金が追加できない or 売却で整理したい場合。

次章では、このポートフォリオ調整の結果をグラフで視覚的にどう読み取るか、また戦略をどう考えていくべきかを扱います。

🔄 次章へのつなぎ

このロジックは、ユーザーが操作可能なツールUIに応用することも可能です。
次章では、このコードをどうユーザーが直感的に使えるようにするかを設計検証していきます。

5. 本ツールの応用と可能性

今回紹介したリスクベースポートフォリオ分析ツールは、以下のような応用が可能です。

▶ 情勢に合わせた調整

利下げ期には債券の割合を増やしたり、価格が低価な高配当株の割合を増やすなど、時代に合わせた設計も可能です。

▶ 新しい銘柄を組み入れる

「今後に買いたい」「興味あるけど価頼性は…」といった未保有の銘柄も、現在の決定に縛られずに評価に組み込むことで、より自分らしい構成を目指せます。

▶ 設定の自動切り替え

年齢や目的により、「能動的にモードを切り替える」ようなユーザー効果も検討中です。たとえば、「買い増しだけ」のモードから、のちのち「売買付き」のモードへ切り替えるなど。

6. まとめ

本シリーズでは、「肩の力を抜けて分散投資を考えるための道具」を目指して、Pythonコードを通した検証を紹介しました。

なぜ分散投資が重要なのか
各銘柄の同動性やクラスタの判断
リスクに基づいた割合の算出
構成の比較表示と解析

これらは、投資に自信を持ち、なおかつデータによる補強を求める方にとって大きな助けとなるはずです。

計算やグラフの出力は、そのままレポートとして法人向けの資産コンサルティングなどに導入することも可能です。

この試みをベースに、更に使い動きやすいツールへの改良も続けていく予定です。

よかったらシェアしてね！

URLをコピーしました！

URLをコピーしました！

この記事を書いた人

shizumaru

Python・投資・業務効率化をテーマにしたブログを運営しています。
本業では社内ツール・アプリの運営・開発をしており、趣味はキャンプや食べ歩きです。

このブログでは、実体験や実務で役立った知識をベースに、
初心者でも再現できる情報発信を心がけています。

コメント一覧（2件）

リスクで見る資産配分：ポートフォリオを構造から見直す方法 - 静かな暮らしとコツコツ資産運用 より:

2025年3月31日 10:17 PM

[…] 👉 続きはこちら：【後編】リスクベースで自動調整！Pythonで構成比を再計算 […]

返信
DTWとKMeansでできる！時系列クラスタリングの基本 - 静かな暮らしとコツコツ資産運用 より:

2025年4月4日 12:24 AM

[…] この記事では、私自身が株価データを使って分析したケースをもとに、実装と解説を行っています。実際の例はこちら：👉 Pythonで資産リバランス：リスクに基づく最適な構成比とは？ […]

返信

Pythonで資産リバランス：リスクに基づく最適な構成比とは？

📌 この記事でわかること：

👤 対象となる読者：

🔧 活用できるシーン：

🔄 次は実践へ：どうリバランスする？

1. Pythonコードとその条件・補足説明

✅ コード①：クラスタリングとリスク分析（ベース分析）

✅ コード②：エルボー法による最適クラスタ数の決定

✅ コード③：リスクベースのポートフォリオ構成比（可視化付き）

🔁 各コードのつながり

🛠️ カスタマイズ可能なポイント

2. 銘柄のクラスタ分析とリスク評価

🔧 使用条件（今回の設定）

💻 フルコード①：クラスタリングとリスク分析

🧠 クラスタごとの分類

📊 リスク（標準偏差）ランキング

🔄 次章へのつなぎ

3. 最適なクラスタ数の検証（エルボー法）

📌 エルボー法とは？

💻 フルコード②：クラスタ数の最適化（エルボー法）

📉 クラスタ数ごとの誤差（SSE）の推移

🔍 補足：クラスタ数の選び方は目的次第

⏭ 次章へのつなぎ

4. 調整モード別ポートフォリオ変化の比較（Before / Adjust / After）

🎯 本章の目的

🔧 分析条件

💻 フルコード③：

✅ 選択モード: both（買い・売り両方で調整）

🎨 調整の可視化

💹 棒グラフ：調整前後の金額比較

🧩 円グラフ：ティッカー別の構成比（Before / After）

🧠 クラスタ別の構成比（Before / After）

🏷️ カテゴリ別の構成比（Before / After）

✅ 選択モード: buy（売却せず、買い増しでのみ調整）

✅ 選択モード: sell（買い増しせず、売却のみで調整）

🔄 次章へのつなぎ

5. 本ツールの応用と可能性

▶ 情勢に合わせた調整

▶ 新しい銘柄を組み入れる

▶ 設定の自動切り替え

6. まとめ

この記事を書いた人

関連記事

コメント

コメント一覧 （2件）

コメントする コメントをキャンセル

コメント一覧（2件）

コメントするコメントをキャンセル