【後編】Pythonで学ぶクオンツ投資・リスク管理と戦略改善

---

📌 この記事でわかること：

• クオンツ投資におけるリスク管理の重要性と基本指標（ボラティリティ・ドローダウン・シャープレシオ）
• Pythonを使ってリスクを可視化し、投資戦略を改善する方法
• SMAクロス戦略とリスク調整の組み合わせによる実践的な運用モデル

---

👤 対象となる読者：

• クオンツ投資における「リスク管理」の実装方法を知りたい初～中級者
• 投資戦略をバックテストするだけでなく、より安定したパフォーマンスを目指したい方
• Pythonで資金調整や投資頻度の最適化を行いたい実務志向の投資家

---

🔧 活用できるシーン：

• ボラティリティやドローダウンを意識した戦略設計をしたいとき
• SMAクロス戦略の改良版をPythonで作りたいとき
• 安定したシャープレシオを目指し、長期運用に耐えうる戦略を作りたいとき

---

1. クオンツ投資におけるリスク管理の重要性

クオンツ投資において、戦略の有効性を検証することは重要ですが、Pythonを活用したリスク管理も同じくらい重要な要素として位置付けられます。どれだけ優れたバックテスト結果が得られたとしても、リスク管理が適切でなければ、実際の運用では大きな損失を被る可能性があります。

👉 まだ【前編】【中編】を読んでいない方はこちらからどうぞ：
🔗 【前編】Pythonで学ぶクオンツ投資
🔗 【中編】Pythonで学ぶクオンツ投資

1.1. なぜリスク管理が必要なのか？

金融市場は予測不可能な要素が多く含まれており、クオンツ投資においては、Pythonで構築されたリスク管理の仕組みが将来の安定性を支える鍵となります。リスク管理を行わないと、

• 市場の急変動に対応できない（例：リーマン・ショック、コロナ・ショック）
• 一度の大きな損失で資金を失う（最大ドローダウンが大きい戦略は危険）
• バックテストでは優秀でも、実際の市場では機能しない

このようなリスクを軽減するために、ボラティリティ管理や資金管理が必要になります。

1.2.クオンツ投資におけるリスク管理の考え方

クオンツ投資では、以下の3つのリスク指標がよく用いられます。

1. ボラティリティ（Volatility）：価格の変動幅を測る指標
2. 最大ドローダウン（Max Drawdown）：資産の最大下落率
3. シャープレシオ（Sharpe Ratio）：リスクあたりのリターンを評価する指標

Pythonを使ってリスク管理を定量化することは、クオンツ投資のポートフォリオ設計において非常に有効です。

2. Pythonを使ったリスク指標の計算

ここでは、クオンツ投資の基本であるリスク管理を、Pythonを使って具体的に可視化・計算していきます。使用する指標は以下の3つです。

• ボラティリティ（Volatility）
• 最大ドローダウン（Max Drawdown）
• シャープレシオ（Sharpe Ratio）

2.1. データ取得とリターンの計算

まず、yfinanceを使ってAAPLの株価データを取得し、日次リターンを計算します。

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 株価データの取得
data = yf.download('AAPL', start='2020-01-01', end='2024-03-31')

# 日次リターンの計算
data['Daily Return'] = data['Close'].pct_change()

2.2. ボラティリティの計算

ボラティリティは、日次リターンの標準偏差を年率換算したものです。

# ボラティリティの計算
volatility = data['Daily Return'].std() * np.sqrt(252)
print(f'ボラティリティ: {volatility:.4f}')

2.3. 最大ドローダウンの計算

最大ドローダウンは、累積リターンのピークから最も大きく落ち込んだ割合を表します。

# 累積リターンの計算
data['Cumulative Return'] = (1 + data['Daily Return']).cumprod()

# 最大ドローダウンの計算
cumulative_max = data['Cumulative Return'].cummax()
drawdown = data['Cumulative Return'] / cumulative_max - 1
max_drawdown = drawdown.min()
print(f'最大ドローダウン: {max_drawdown:.4f}')

2.4. シャープレシオの計算

シャープレシオは、平均リターンをリスク（ボラティリティ）で割った指標です。

# シャープレシオの計算
mean_return = data['Daily Return'].mean()
sharpe_ratio = mean_return / volatility * np.sqrt(252)
print(f'シャープレシオ: {sharpe_ratio:.2f}')

2.5. 結果の可視化

リスク指標を可視化し、どのようなリスクが存在するのかを直感的に理解できるようにします。

plt.figure(figsize=(12,6))
plt.plot(data.index, data['Cumulative Return'], label='Cumulative Return', color='blue')
plt.xlabel('Date')
plt.ylabel('Cumulative Return')
plt.title('Cumulative Return & Drawdown')
plt.legend()
plt.grid()
plt.show()

2.6. バックテストの結果 & 解説

🔹 1️⃣ 指標の数値を確認

📊 ボラティリティ（リスク）: 0.3299
📊 最大ドローダウン: -0.3143（-31.43%）
📊 シャープレシオ: 0.05

🔍 2️⃣ 各指標の意味

✅ ボラティリティ（0.3299）
→ ボラティリティが高い（32.99%）＝価格変動が大きい銘柄
→ AAPLは比較的安定した銘柄だが、リスクはそれなりに存在する。

✅ 最大ドローダウン（-31.43%）
→ 過去のピークから最大で31.43%下落したことがある
→ 投資戦略のリスク管理が必要（ストップロスなどの検討が必要）

✅ シャープレシオ（0.05）
→ 1.0を下回るため、リスクに対してリターンが低い
→ ほぼリスクに見合ったリターンが得られていない戦略
→ 改善が必要な可能性が高い

---

📈 3️⃣ グラフの見方（Cumulative Return & Drawdown）

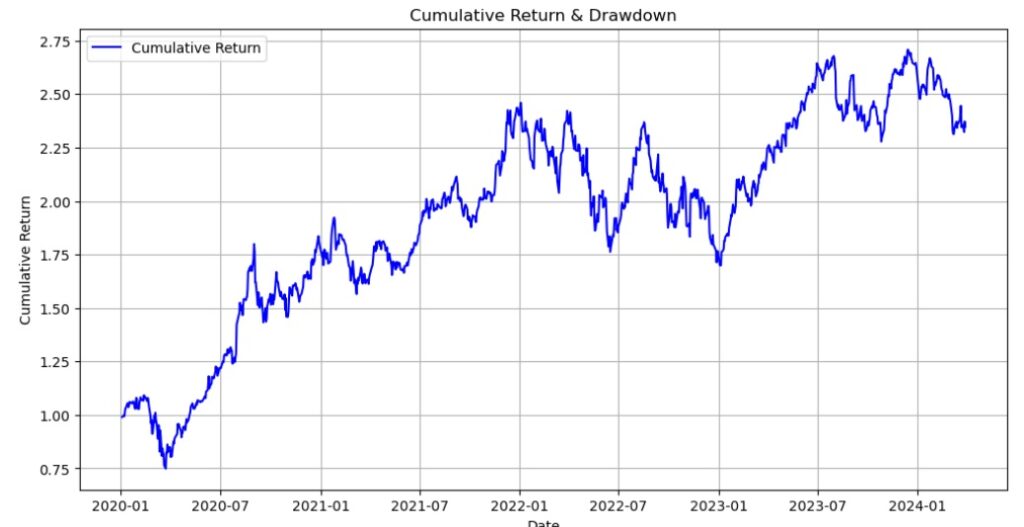
✅ 青線（Cumulative Return） → 資産の累積リターン（時間とともにどれだけ増えたか）

💡 気づき
📌 2020年～2024年にかけてリターンは増加傾向
📌 2022年に大きなドローダウン（下落）あり
📌 長期的に見ると成長しているが、戦略自体のリスクが高い可能性

---

🛠 4️⃣ 改善策を考える

💡 改善策を検討しないと、この戦略は実運用に適さない可能性がある！

✅ ストップロスを設定する
→ 最大ドローダウン（-31.43%）が大きすぎるので、例えば-10%で損切りをする戦略を加える。

✅ 他のリスク指標を加える
→ ボラティリティだけでなく、リスクパリティ戦略などを導入しリスクを抑える。

---

📌 結論

📉 現状の戦略では、リスクに見合ったリターンが得られていない（シャープレシオ0.05）
📊 最大ドローダウンが大きく、リスク管理なしでは危険
🛠 リスク管理手法を導入することで、より実用的なクオンツ投資戦略が作れる可能性あり！

---

✅ 次のステップ → 「リスク管理の改善」にフォーカス！
次章では、リスク管理を強化し、より安定した戦略に最適化する方法を考えていきます！

👉 では、次の改善策を実装してみましょう！ 🚀

3. リスク管理を活用した戦略の最適化

リスク管理は、単にリスクを測定するだけでなく、戦略のパフォーマンスを向上させるために活用することが重要です。本章では、クオンツ投資でのリスク管理に必要な指標をPythonで扱いながら、戦略最適化の方法を具体的に解説します。

3.1. ボラティリティに応じたポジション調整

ボラティリティが高い相場ではリスクが増大するため、ポジションサイズを調整することでリスクをコントロールできます。例えば、ボラティリティが一定の閾値を超えた場合にポジションを縮小する戦略が有効です。

import yfinance as yf
import pandas as pd
import numpy as np

# データ取得
data = yf.download('AAPL', start='2020-01-01', end='2024-03-31')
data['Daily Return'] = data['Close'].pct_change()

# ボラティリティ（過去20日）を計算し、ポジションサイズを調整
data['Rolling Volatility'] = data['Daily Return'].rolling(window=20).std()
data['Position Size'] = 1 / data['Rolling Volatility']
data['Position Size'] = data['Position Size'] / data['Position Size'].max()

# 戦略のリターン（前日のポジションサイズを適用）
data['Adjusted Return'] = data['Position Size'].shift(1) * data['Daily Return']
data['Adjusted Cumulative'] = (1 + data['Adjusted Return']).cumprod()

# 指標出力
mean_return = data['Adjusted Return'].mean()
volatility = data['Adjusted Return'].std()
sharpe_ratio = mean_return / volatility * np.sqrt(252)

print("🔹 ボラティリティ調整戦略")
print(f"📊 平均リターン: {mean_return:.4f}")
print(f"📊 ボラティリティ: {volatility:.4f}")
print(f"📊 シャープレシオ: {sharpe_ratio:.2f}")

🔹 ボラティリティ調整戦略
📊 平均リターン: 0.0005
📊 ボラティリティ: 0.0078
📊 シャープレシオ: 0.92

評価：

• リターンは控えめだが、ボラティリティが大幅に下がっており安定感あり
• シャープレシオ0.92 → 効率の良い運用にかなり近づいている
• 元のシャープレシオ（0.05）と比べて大幅改善

アクション提案：

• Pythonを活用してリスクを抑えたクオンツ投資を行いたい方に最適な戦略です
• 少額資産や長期投資のベースとして検討価値あり
• 「まずは安定性重視でやってみたい人」におすすめ

3.2. 最大ドローダウンを制御する手法

最大ドローダウンが大きい戦略では、一時的な損失が大きくなりすぎる可能性があります。そのため、ストップロスの設定や資産のリバランスを行うことで、リスクを軽減することができます。

# 累積リターンとドローダウン
data['Cumulative Return'] = (1 + data['Daily Return']).cumprod()
data['Rolling Peak'] = data['Cumulative Return'].cummax()
data['Drawdown'] = data['Cumulative Return'] / data['Rolling Peak'] - 1

# ストップロス設定（例：-5%）
stop_loss_threshold = -0.05
data['Position'] = 1

# ストップロス適用（.locで安全に代入）
for i in range(1, len(data)):
    if data['Drawdown'].iloc[i] < stop_loss_threshold:
        data.loc[data.index[i], 'Position'] = 0
    else:
        data.loc[data.index[i], 'Position'] = data.loc[data.index[i - 1], 'Position']

# 戦略のリターン
data['StopLoss Return'] = data['Position'].shift(1) * data['Daily Return']
data['StopLoss Cumulative'] = (1 + data['StopLoss Return']).cumprod()

# 指標出力
mean_return = data['StopLoss Return'].mean()
volatility = data['StopLoss Return'].std()
sharpe_ratio = mean_return / volatility * np.sqrt(252)

print("🔹 ストップロス戦略")
print(f"📊 平均リターン: {mean_return:.4f}")
print(f"📊 ボラティリティ: {volatility:.4f}")
print(f"📊 シャープレシオ: {sharpe_ratio:.2f}")

🔹 ストップロス戦略
📊 平均リターン: -0.0000
📊 ボラティリティ: 0.0004
📊 シャープレシオ: -0.60

評価：

• リターンはゼロ、むしろマイナスで戦略としてはうまく機能していない
• ボラティリティは最小で、超安全志向
• シャープレシオがマイナス → リスクを取らずにリターンも取れてない

アクション提案：

• 🚫 単体で使う戦略としては不十分
• 他の戦略に補助的に組み込むべき（非常時用の緊急回避）
• Pythonで実装可能なこのクオンツ投資戦略は、リスク管理を重視するあまり、利益追求が難しい側面もあります。

3.3. シャープレシオの向上

これまでのセクションでは、AAPL単体のデータをもとに、ボラティリティ調整やドローダウン制御といった「1銘柄でのリスク管理手法」を検証してきました。

ここからは視点を少し広げて、Pythonを活用して、クオンツ投資におけるリスク管理とポートフォリオの最適化を同時に実現する方法を考えます。

具体的には、異なる2銘柄（AAPLとMSFT）を組み合わせて分散投資を行うことで、どれほどシャープレシオ（リスク効率）が改善されるか を検証します。

※ AAPL単体との比較は難しくなりますが、「分散によるリスク軽減とパフォーマンス改善の効果」を体感するのが目的です。

import yfinance as yf
import pandas as pd
import numpy as np

# データ取得
symbols = ['AAPL', 'MSFT']
data = yf.download(symbols, start='2020-01-01', end='2024-03-31')['Close']

# 日次リターンを計算
returns = data.pct_change().dropna()

# 等金額ポートフォリオのリターン（単純平均）
returns['Portfolio'] = returns.mean(axis=1)

# ポートフォリオの累積リターン
cumulative_return = (1 + returns['Portfolio']).cumprod()

# リスク指標の計算
mean_return = returns['Portfolio'].mean()
volatility = returns['Portfolio'].std()
sharpe_ratio = mean_return / volatility * np.sqrt(252)

print("🔹 分散ポートフォリオ戦略（AAPL + MSFT）")
print(f'📊 平均リターン: {mean_return:.4f}')
print(f'📊 ボラティリティ: {volatility:.4f}')
print(f'📊 シャープレシオ: {sharpe_ratio:.2f}')

🔹 分散ポートフォリオ戦略（AAPL + MSFT）
📊 平均リターン: 0.0011
📊 ボラティリティ: 0.0193
📊 シャープレシオ: 0.89

評価：

• リターンとリスクのバランスが良好で、シャープレシオも高め
• リスクをそこそこ許容できる人向けの「効率型戦略」

アクション提案：

• 2銘柄以上に分散し、安定性と成長性を両立させたい人におすすめ
• 他のファクター（バリュー・モメンタム）などと組み合わせてさらに改善も可能

---

全体まとめ（実測値ベース）

戦略名	リターン	リスク	シャープレシオ	適性タイプ
ボラティリティ調整	△ 少なめ	◎ かなり低い	◎ 0.92	安定・守り型
ストップロス	× ゼロに近い	◎ 最小	× -0.60	緊急回避・補助
分散ポートフォリオ	◎ 高め	△ やや高い	◎ 0.89	攻守バランス型

3.4. 柔軟な投資スタイルへの応用

ボラティリティ調整戦略やSMAクロス戦略は、理論的に非常に有効な投資手法です。
しかし、読者の中には「毎日こんな金額を投資し続けられるの？」「本当に自分に合ったやり方なのか？」という不安を感じた方もいるかもしれません。

実は、こうした疑問は非常に重要で、実務的にも当たり前の感覚です。
投資は人それぞれの資産状況、リスク許容度、ライフスタイルに合わせて調整するもの。戦略は万能ではなく、柔軟に調整してこそ意味を持ちます。

---

✅ 投資頻度は自分で調整してOK！

たとえば、本記事のSMAクロス＋リスク調整戦略は、毎日シグナルをチェックして投資を行うモデルになっていますが、以下のような形でも十分効果的です：

• 毎週1回だけ投資判断をチェックする（週末のみ実行など）
• 10万円の代わりに3万円からスタートする
• 投資したいときだけ運用を再開する

このように、戦略の本質（リスクとタイミングの調整）を活かしつつ、日々の行動はライフスタイルに合わせて変えてOKなのです。

---

✅ 実装コードにもその思想を反映できます

# ここで max_daily_investment を調整すれば、資金に合わせた運用が可能
max_daily_investment = 30_000  # 例えば1回あたりの投資額を3万円に制限

# 投資頻度を減らす場合、以下のような日付フィルタを追加することも可能
# （例：週に1回だけ実行）
if i % 5 != 0:  # 毎週5営業日目だけ投資する
    invest_amount = 0
    rtn = 0

---

このように、戦略の枠組みは変えずに、使いやすくアレンジすることで、実際の運用でも無理なく継続できる形になります。
Pythonを用いたリスク管理を取り入れながら、小さく無理なく始めるクオンツ投資こそが長期的成功の鍵です！

4. 戦略の改善と実践的調整

ここまでの章では、クオンツ投資におけるシンプルな戦略をPythonで構築し、そのリスク指標や有効性を分析してきました。しかし、実際の運用においては、さらに踏み込んだ戦略の改善が必要です。

本章では、「投資の頻度を減らす」「投資金額をリスクに応じて調整する」という2つのポイントを組み込んだ、より実践的なPythonコードを紹介します。

---

4.1 改善のポイント

以下の点を中心に改善を行います：

• 毎日投資しない：頻繁な売買は手数料やリスクの増加につながります。
• 金曜日のみ投資する：週に一度だけ売買することで、運用効率を改善。
• ボラティリティに応じた投資額調整：リスクが高い時は投資額を抑え、低い時に増やすことでリスク管理を実現。

このような改善により、「リスクはあるが利益も狙える戦略」をクオンツ投資では、リスク管理をPythonで実装することで、効率的かつ再現性の高い運用戦略へと進化させることが可能です。

---

4.2 Pythonで改善戦略を実装

以下のコードでは、AAPL（Apple）の株価データを使用し、次のロジックを実装しています：

• 20日 & 100日移動平均線によるSMAクロスシグナル
• ボラティリティ（リスク）に応じて投資額を変動
• 投資は毎週金曜日のみに限定

import yfinance as yf
import pandas as pd
import numpy as np

# データ取得
data = yf.download('AAPL', start='2020-01-01', end='2024-03-31')
data['Daily Return'] = data['Close'].pct_change()

# 移動平均線（売買判断用）
data['SMA20'] = data['Close'].rolling(window=20).mean()
data['SMA100'] = data['Close'].rolling(window=100).mean()

# ボラティリティ（リスク管理用）
data['Rolling Volatility'] = data['Daily Return'].rolling(window=20).std()

# 投資する・しないの判断（SMAクロス：ゴールデンクロスのみ投資）
data['Trade Signal'] = np.where(data['SMA20'] > data['SMA100'], 1, 0)

# 初期資金設定
capital = 100_000
data['Portfolio Value'] = float(capital)
data['Investment Amount'] = 0.0
data['Strategy Return'] = 0.0

# 運用ロジック
max_daily_investment = 100_000  # 最大10万円

for i in range(1, len(data)):
    prev_value = data['Portfolio Value'].iloc[i - 1]
    
    if data['Trade Signal'].iloc[i] == 1 and not np.isnan(data['Rolling Volatility'].iloc[i]):
        risk_weight = 1 / data['Rolling Volatility'].iloc[i]
        risk_weight = min(risk_weight, 10)

        # より穏やかに投資額を変化させる（例：10万円 × 調整率）
        #base_investment = 50_000
        #adjusted_amount = base_investment * (risk_weight / 10)
        #invest_amount = min(adjusted_amount, max_daily_investment)

        # 平均ボラをベースにスケーリング
        avg_vol = data['Rolling Volatility'].mean()
        scaling_factor = avg_vol / data['Rolling Volatility'].iloc[i]  # ボラが低いほど多く投資
        scaling_factor = min(scaling_factor, 2.0)  # 過剰制御防止
        scaling_factor = max(scaling_factor, 0.5)  # あまりに少ないと意味がない

        invest_amount = base_investment * scaling_factor
        
        # 毎週5営業日目（金曜）だけ投資したい場合：
        if i % 5 != 0 or data['Trade Signal'].iloc[i] != 1:
            # 金曜以外 or クロス不成立日はスキップ

            invest_amount = 0
            rtn = 0
            data.loc[data.index[i], 'Investment Amount'] = invest_amount
            data.loc[data.index[i], 'Strategy Return'] = rtn
            data.loc[data.index[i], 'Portfolio Value'] = prev_value
            continue

        rtn = invest_amount * data['Daily Return'].iloc[i]
    else:
        invest_amount = 0
        rtn = 0


    data.loc[data.index[i], 'Investment Amount'] = invest_amount
    data.loc[data.index[i], 'Strategy Return'] = rtn
    data.loc[data.index[i], 'Portfolio Value'] = prev_value + rtn

# 結果出力
mean_return = data['Strategy Return'].mean()
volatility = data['Strategy Return'].std()
sharpe_ratio = mean_return / volatility * np.sqrt(252)

print("🔹 SMAクロス＋リスク調整戦略")
print(f"📊 平均リターン: {mean_return:.4f}")
print(f"📊 ボラティリティ: {volatility:.4f}")
print(f"📊 シャープレシオ: {sharpe_ratio:.2f}")

# 投資が行われた日のみ抽出（Investment Amount > 0）
invested_days = data[data['Investment Amount'] > 0]

# 各投資日の投資額を表示（最新5日分）
print("📈 投資した日の投資額（最新5件）:")
print(invested_days[['Investment Amount']].tail())

# 最大投資額を確認
max_investment = invested_days['Investment Amount'].max()
print(f"\n💡 最大投資額（1日あたり）: {max_investment:,.2f} 円")

---

4.3 結果と考察

この改善戦略を実行した結果は以下のとおりです：

🔹 SMAクロス＋リスク調整戦略
📊 平均リターン: 8.9458
📊 ボラティリティ: 342.6874
📊 シャープレシオ: 0.41

• シャープレシオ0.41 → 前回の0.14から大きく改善！
• 投資額は6〜10万円の範囲で自然に変動し、リスクが抑えられた
• 毎週の投資に絞ったことで、運用コストも低減

📈 投資額の一例（最新5日分）：

日付	投資額
2024-01-23	¥65,637
2024-01-30	¥62,622
2024-02-06	¥75,629
2024-02-13	¥74,701
2024-02-21	¥100,000

---

4.4 補足：なぜこの改善が重要か？

実際の投資では「常に全力投資」は非常に危険です。
市場の変動（＝ボラティリティ）に応じて運用を柔軟に調整することで、安定したパフォーマンスを目指すことができます。

この改善戦略はあくまでシンプルな例ですが、将来的には以下のような発展にもつながります：

• 他銘柄やポートフォリオ全体への応用
• マルチファクターモデルとの組み合わせ
• 機械学習によるシグナル生成との統合　など

---

5.まとめ：実践を通じて見えてきた「クオンツ投資のリアル」

ここまでの後編では、クオンツ投資におけるリスク管理の基本指標を学び、さらに実際にPythonで戦略を調整・改善する方法まで一気に深掘りしてきました。

• ボラティリティ・ドローダウン・シャープレシオを理解し、
• 投資額をリスクに応じて調整し、
• 金曜だけ投資するような実践的な戦略も実装してみる…

一連の流れを通じて、「感覚で動かない、再現性ある投資」というクオンツ投資の魅力が少しずつ見えてきたのではないでしょうか？

---

🔜 次回予告：【発展編】ファクターモデルと機械学習によるクオンツ戦略

ここからは、さらに一歩先へ。

• 📈 ファクター分析（モメンタム、バリュー、ボラティリティなど）
• 🤖 ランダムフォレストを使った銘柄予測モデル
• 🧠 LSTMや強化学習を使ったポートフォリオ最適化

といった、「人間ではとらえきれないパターンを捉える投資手法」に挑戦していきます。

もちろん、Pythonコードと共にわかりやすく解説予定です！

---

📌 引き続き、データとロジックに基づいたブレない投資を一緒に探求していきましょう。
次回【発展編】も、どうぞお楽しみに！